2nd Semester Summary

This semester at first was very difficult for me. I didn't d to well on my tests and quizzes and the material was very challenging to understand. As the semester went on, I began to understand the material better and my tests scores went up gradually. This summer, I will be looking at note colleges across the U.S. and go to see my relatives in Boston. I probably will also go to the beach a lot and spend some quality time with my friends and family just relaxing. I am also going to be doing a lot of SAT prep this summer and be doing more and more MATH yahhhhhhh!!!! But I can't wait until finals are over and I can take a break from studying. 

Trig review week

This week I relearned how to do partial fraction decompositions, SOH-COA-TOA, parametric equations, double angles and half angles. For parametric equations I learned the steps again, for example graphing and eliminating the parameter when solving for the rectangular equation. Also, doing a t,x,y chart and plotting x and y coordinate pairs to form a graph. I also learned verifying and solving trig equations and that when verifying we make one side look like the other side. And for solving trig equations we set x equal to a certain radian measure and look where that radian measure is on the unit circle and those radian measures are the solutions to the problems. Lastly, I relearned the binomial theorem and how Pascals Triangle relates to the Binomial Theroem and helps solve the questions more easily. 

Repeating decimals

A repeating or recurring decimal is a way of representing rational numbers in base 10 arithmetic. The decimal representation of a number is said to be repeating if it becomes periodic (repeating its values at regular intervals) and the infinetely - repeated portion is not zero. The infinitely-repeated digit sequence is called the repeated or reptend. If the repetend is a zero, this decimal representation is called a terminating decimal rather than a repeating decimal, since the zeros can be omitted and the decimal terminates before these zeros. Steps for solving: write as a geometric series, and lastly find the sum. The sum formula is s=a1/1-r. 

Parametric equations

In mathematics, parametric equations of a curve express the coordinates of the points of the curve as functions of a variable, called a parameter. For example, x=cos ty=sin t. These are parametric equations for the unit circle, where t is the parameter. Each value of t defines a point (x, y)= (f(t), g(t)) that we can plot. The collection of points that we get by letting t be all possible values is the graph of the parametric equations and is called the parametric curve. Steps to solve parametric equations include sketching the graph and eliminating the parameter. For graphing you want to write a t,x,y chart and solve for the x, y pairs to graph. For eliminating the parameter, you want to either use the trig identities or use elimination or substitution to solve for the rectangular equation. 

 

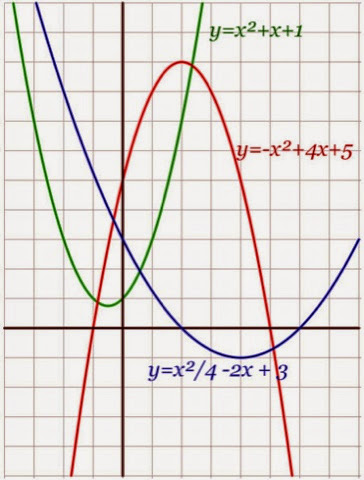
Systems of equations

A system of equations is a set of two or more equations that you deal with at one time. When solving the system, you must consider all of the equations involved and find a solution that satisfies all of the equations. When you graph a system, the point of interesection is the solution. A linear system of equations will only have one solution, and that is the point of intersection. Although, as always, there are times when you will find no solution or an infinte number of solutions. When a linear system has no solution, then the lines are parallel. If a linear system has an infinite amount of solutions, then the lines are the same. 

Partial Fraction Decomposition

For partial fraction decomposition, your either going to be solving it as a linear or quadratic problem. The steps include first multiply by the LCD. Second group terms by powers of x. Lastly, equate coefficients and solve the system of equations. If the degree of the numerator is bigger than the degree of the denominator then we will be using long division. And when it's a quadratic problem, we write Bx+C as the numerator. 

Probability of an Event

In probability theory, an event is a set of outcomes of an experiment, to which a probability is assigned. A single outcome may be an element of many different events, and different events in an experiment are usually not equally likely, since they may include very different groups of outcomes. In words, this means that the probability of an event must be a number between 0 and 1(inclusive). Also, probability of an impossible event is always zero. On the other hand, the probability of an impossible event is always zero. 

Recursion and mathematical Induction

In the Tower of Hanoi Puzzle, I learned how many different possible methods of moving the rings around. I decided to move the first ring to the middle, so that I could get the other rings to the far side. However, it became difficult because the rings had to be stacked from greatest on the bottom to the smallest on the top. Because of this, I couldn't stack the third ring first and then the fourth on top. I had to make smart choices of where I would place each ring because there were many obstacles and rules in the puzzle itself. I also learned many things from recursion and mathematical induction such as that n always equals one and then we must assume that the statement is held true for n equals k, and also prove it true for k+1. When solving the proof for the Tower of Hanoi Puzzle, the general equation was Tn=2 to the n exponent minus one. The first step was that I had to show this true for n=1 and I had to explain why this was true. The second step was that I assumed true for n=k and I substituted k in for n. Lastly I had to show true for Tk+1 and plug in k+1 for n in the equation. I was able to solve and prove the proof was correct. 

Sequences and Series

A sequence can be described as a list of objects, events, or numbers that come one after the other, that is, a list of things given in some definite order. Each object in the list is called a term of the sequence. Where no last term is indicated, is understood to be an infinite sequence. The three dots is called an ellipsis amd indicates that succeeding terms follow the same pattern as that set by the terms given. The elements in the range of a sequence are simply the terms of the sequence. The nth term f(n)=an is also called the general term of the sequence. 

Graphing Systems of Inequalities

To graph systems of inequalities there are certain rules that must be followed. First, solid lines are used when the inequality could be equal to, dashed lines are for strict inequality. Second, when a line is in slope-intercept form, shading is above the line when it is greater than and the shading is below the line when it is lesser than. When a line is in standard form, the shading is the same as it is in slope-intercept form if the coefficient of the y-variable is positive, otherwise it is reversed. When working with standard form, it is sometimes necessary to choose better numbers to ensure the graph is precise. 

Cramer's Rule

In linear algebra, Cramer's rule is an explicit formula for the solution of a system of linear equations with as many equations as unknowns, valid whenever the system has a unique soltution. It expresses the solution in terms of the determinants of the coefficient matrix and of matrices obtained from it by replacing one column by the vector of right hand sides of the equations. It is named after Gabriel Cramer, who published the rule for an arbitrary number of unknowns in 1750. The rule holds for systems of equations with coefficients and unknowns in any field, not just in the real numbers. It has recently been shown that Cramer's rule can be implemented in O(n³) time, which is comparable to more common methods of solving systems of linear equations, such as Gaussian Elimination. 

Graphs of Polar Equations

There are many different types of polar graphs such as limacons, rose curves, circles and lemniscates. The four different types of Limacons are: limacons with inner loop, cardioid (heart-shaped), dimpled limacons and convex limacons. There are also four different types of rose curves: two with r=acosnfeta and two with r=asinnfeta. There are also two different types of circles: r=acosfeta and r=asinfeta. Lastly there are two different types of lemniscates: r squared= a squared sin2feta and r squared=a squared cos2feta. For limacons a must be greater than zero and b must be greater than zero. For rose curves: the number of petals if the number is odd, and two times the number of petals if the number is even, the number of petals is equal or greater than two. 

Polar Coordinares

The polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a fixed point and an angle from a fixed direction. The fixed point is called the pole, and the ray from the pole in the fixed direction is the polar axis. The distance from the pole is called the radical coordinate or radius, and the angle is the angular coordinate, polar angle, or azimuth. When feta is bigger than zero than it's counterclockwise and if feta is less than zero than it's clockwise. Polar coordinates are written as (r, feta). 

Rotation of Conics

We use the equation Ax^2+Bxy+Cy^2+Dx+Ey+F=0 to solve conic sections. When B=0, we obtain the standard forms of equations of circles, parabolas, ellipses, and hyperbolas. Degenerate cases might be represented and that's when two interesting lines, one line, a single point, two parallel lines, or no graph at all appears. When B doesn't equal zero then it is possible to remove the xy-term in equation (1) by a rotation of axes. Therefore it is always possible to select the angle of rotation so that any equation of the form (1) can be transformed into an equation in x' Andy ' with no x'y'-term: A'(x)^2+C'(y')^2. 

Parabola

There are two types of parabolas. A parabola with (x-h)^2=4c(y-k)  form and a parabola with (y-k)^2=4c(x-h). The first parabola has a vertex of (h,k), focus of (h, k+c), directrix of y=k-c and axis of symmetry of x=h. The second parabola has a vertex of (h, k), focus of (h+c, k), directrix of x=h-c, and axis of symmetry of y=k. For both graphs the value of c can be greater than or less than zero. You do the y-intercept if your given an equation of (x-h) and you find the x-intercept if you are given an equation of (y-k). The standard form of the equation of a parabola with focus (0, c), directrix y=-c, c>0, and vertex (0, 0). 

Blog for first week back from winter break

3 things you did well:

The first thing that I did well last semester was staying on top of my homework on webassign and not getting behind on homework. The second thing is studying hard for all my tests and quizzes and asking the teacher for help when I didn't understand something I was studying. The third thing is taking good notes in class and listening to the teacher as much as possible. 

3 goals to improve on: 

The first goal is to get better grades on my tests and quizzes. The second goal is to try different studying styles and to see if they benefit me or not. The third goal is to have more confidence in myself and to not give up when the class becomes difficult. 

Favorite Christmas Story: 

My favorite Christmas story is The Night Before Christmas with the mouses and not a creek of noise.